X IPS 2
Fungsi Invers
Diketahui f -1 (4x-5) = 3x-1 dan (f -1 ◦ f)(5)= p2 +2p – 10 maka rata-rata dari nilai p adalah…
- -4
- -2
- -1
- 1
- 4
Jawab:
f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
Menentukan nilai p
(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
Sehingga, rata-rata nilai p yaitu 

Jawaban : C
Contoh Soal 5
Tentukan rumus fungsi invers dari fungsi f(x) = 2x + 6.
Jawab:

Contoh Soal 6
Tentukan rumus fungsi invers dari fungsi 

Jawab:

Contoh Soal 7
Diketahui  jika
jika  adalah invers dari f, maka
adalah invers dari f, maka = ...
= ...
a. 2/3 (1 + x)
b. 2/3 (1 – x)
c. 3/2 (1 + x)
d. – 3/2 (x – 1)
e. – 2/3 (x + 1)
Pembahasan
Ingat rumus ini ya: jika , maka:
, maka:

Jawaban : A
 jika
jika  adalah invers dari f, maka
adalah invers dari f, maka = ...
= ...a. 2/3 (1 + x)
b. 2/3 (1 – x)
c. 3/2 (1 + x)
d. – 3/2 (x – 1)
e. – 2/3 (x + 1)
Pembahasan
Ingat rumus ini ya: jika
 , maka:
, maka:
Jawaban : A
Contoh Soal 8
Diketahui f(x) = x + 4 dan g(x) = 2x maka  = ...
= ...
a. 2x + 8
b. 2x + 4
c. ½ x – 8
d. ½ x – 4
e. ½ x – 2
Pembahasan
(f o g)(x) = f(g(x))
= f(2x)
= 2x + 4
Kita cari invers dari (f o g)(x) yaitu:
(f o g)(x) = 2x + 4
y = 2x + 4
2x = y – 4
x = (y-4)/2
x = ½ y – 2
maka, = ½ x – 2
= ½ x – 2
Jawaban : E
 = ...
= ...a. 2x + 8
b. 2x + 4
c. ½ x – 8
d. ½ x – 4
e. ½ x – 2
Pembahasan
(f o g)(x) = f(g(x))
= f(2x)
= 2x + 4
Kita cari invers dari (f o g)(x) yaitu:
(f o g)(x) = 2x + 4
y = 2x + 4
2x = y – 4
x = (y-4)/2
x = ½ y – 2
maka,
 = ½ x – 2
= ½ x – 2Jawaban : E
Contoh Soal 9

Contoh Soal 10
Contoh Soal 11
Jika  dan f-1 invers dari f, maka
dan f-1 invers dari f, maka  (x) = -4 untuk nilai x sama dengan ...
(x) = -4 untuk nilai x sama dengan ...
a. -2
b. 2
c. – ½
d. -3
e. – 1/3
Pembahasan
Kita pakai rumus: jika

-2x + 1 = -4x
-2x + 4x= -1
2x = -1
x = - ½
Jawaban : C
 dan f-1 invers dari f, maka
dan f-1 invers dari f, maka  (x) = -4 untuk nilai x sama dengan ...
(x) = -4 untuk nilai x sama dengan ...a. -2
b. 2
c. – ½
d. -3
e. – 1/3
Pembahasan
Kita pakai rumus: jika


-2x + 1 = -4x
-2x + 4x= -1
2x = -1
x = - ½
Jawaban : C
Contoh Soal 12
Contoh Soal 13
Diketahui  , x ≠ 5/6 dan fungsi invers dari f(x) adalah
, x ≠ 5/6 dan fungsi invers dari f(x) adalah  (x). Nilai dari
(x). Nilai dari  (2) = ...
(2) = ...
a. 14/3
b. 17/14
c. 6/21
d. – 17/14
e. – 14/3
Pembahasan
Kita pakai rumus: jika


Jawaban : C
 , x ≠ 5/6 dan fungsi invers dari f(x) adalah
, x ≠ 5/6 dan fungsi invers dari f(x) adalah  (x). Nilai dari
(x). Nilai dari  (2) = ...
(2) = ...a. 14/3
b. 17/14
c. 6/21
d. – 17/14
e. – 14/3
Pembahasan
Kita pakai rumus: jika



Jawaban : C
Contoh Soal 14
Contoh Soal 15













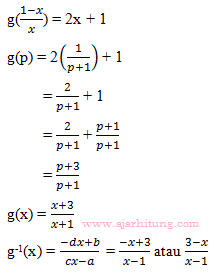









 dalam interval 0 ≤ x ≤ 2π
dalam interval 0 ≤ x ≤ 2π 

