SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN TURUNAN

Indah Putri Lestari (17)

XI IPS 2

Matematika

SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN TURUNAN

1. Suatu perusahaan memproduksi $x$ unit barang dengan biaya $(4x^2-8x+24)$ ribu rupiah untuk tiap unit.  Jika barang tersebut terjual habis dengan harga Rp40.000,00 untuk tiap unit, maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah...

a. Rp16.000,00                    d. Rp52.000,00
b. Rp32.000,00                    e. Rp64.000,00
c. Rp48.000,00

Pembahasan

Misalkan $f\left(x\right)$ menyatakan total biaya produksi $x$ unit barang, $g\left(x\right)$ menyatakan harga jual $x$ unit barang dalam satuan ribu rupiah, dan $h\left(x\right)$ menyatakan keuntungan yang diperoleh atas penjualan $x$ unit barang, maka
$\begin{array}{cc}f\left(x\right)& =x(4x^2-8x+24)\\ & =4x^3-8x^2+24x\\ g\left(x\right)& =40x\\ h\left(x\right)& =g\left(x\right)-f\left(x\right)\\ & =40x-(4x^3-8x^2+24x)\\ & =-4x^3+8x^2+16x\end{array}$
Agar maksimum, nilai turunan pertama $h^{\prime }\left(x\right)$ harus bernilai $0$. 
$\begin{array}{cc}h\left(x\right)& =-4x^3+8x^2+16x\\ h^{\prime }\left(x\right)& =-12x^2+16x+16\\ 0& =-12x^2+16x+16\\ \text{Bagi}& \text{kedua ruas dengan -4}\\ 0& =3x^2-4x-4\\ 0& =(3x+2)(x-2)\end{array}$
Diperoleh $x=-\frac{2}{3}$ atau $x=2$. Karena $x$ menyatakan jumlah barang dan nilainya tidak mungkin negatif/pecahan, maka $x$ yang diambil adalah $x=2$. 
Substitusikan $x=2$ ke $h\left(x\right)$. 
$\begin{array}{cc}h\left(2\right)& =-4(2{)}^3+8(2{)}^2+16\left(2\right)\\ & =-4\left(8\right)+8\left(4\right)+32=32\end{array}$
Jadi, keuntungan maksimum yang diperoleh perusahaan tersebut adalah Rp32.000,00.
(Jawaban B)

2. Sebuah peluru ditembakkan ke atas. Jika tinggi $h$ meter setelah $t$ detik dirumuskan dengan $h\left(t\right)=120t-5t^2$,maka tinggi maksimum yang dicapai peluru tersebut adalah...meter. 

a. $270$                     c. $670$                  e. $770$
b. $320$                     d. $720$   

Pembahasan

Diketahui: $h\left(t\right)=120t-5t^2$. 
Turunan pertama fungsi $h$ adalah
$h^{\prime }\left(t\right)=120-10t$
Nilai $t$ akan maksimum saat $h^{\prime }\left(t\right)=0$, sehingga ditulis
$120–10t=0\iff 10t=120\iff t=12$
Ketinggian maksimum yang dapat dicapai peluru adalah saat $t=12$, yaitu
$\begin{array}{cc}h\left(12\right)& =120\left(12\right)-5(12{)}^2\\ & =1440-720=720\end{array}$ 
Jadi, ketinggian maksimum peluru adalah $720\text{meter}$
(Jawaban D)

3. Sebuah taman berbentuk persegi panjang dengan keliling $(2x+24)$ meter dan lebar $(8-x)$ meter. Agar luas taman maksimum, panjang taman tersebut adalah...meter. 

a. $4$                      c. $10$                  e. $13$
b. $8$                      d. $12$         

Pembahasan 

Panjang taman tersebut dapat ditentukan dengan menggunakan keliling dan lebarnya. 
$\begin{array}{cc}k& =2(p+l)\\ 2x+24& =2(p+8-x)\\ x+12& =p+8-x\\ p& =2x+4\end{array}$
Nyatakan luas persegi panjang sebagai fungsi terhadap variabel $x$.
$\begin{array}{cc}L\left(x\right)& =p\times l\\ & =(2x+4)(8-x)\\ & =-2x^2+12x+32\end{array}$ 
Luas akan maksimum saat $L^{\prime }\left(x\right)=0$, sehingga
$\begin{array}{cc}{L}^{\prime }\left(x\right)& =0\\ -4x+12& =0\\ 4x& =12\\ x& =3\end{array}$
Saat $x=3$, diperoleh
$\begin{array}{cc}p& =2x+4\\ p& =2\left(3\right)+4=10\end{array}$
Jadi, panjang taman tersebut adalah $10\text{meter}$
(Jawaban C)

4. Turunan pertama dari   adalah ...

Pembahasan


(Jawaban D)

5. Diketahui  dan f’ adalah turunan pertama f. Nilai f’(1) adalah      ...

     a.    3
     b.    8
     c.    13
     d.    16
     e.    21

Pembahasan


              = 3 – 20 + 25
              = 8
(Jawaban B)

6. Jika dengan f’ adalah turunan pertama f, maka nilai f’(2) adalah ...
    a.    5
    b.    20
    c.    30
    d.    40
    e.    50

Pembahasan
Kita gunakan rumus ini ya: 


               = 20.1
               = 20
(Jawaban B)

7. Diketahui , nilai dari f’(5) adalah ...
    a.    6
    b.    10
    c.    14
    d.    17
    e.    20

Pembahasan

    f’(x) = 2x + 4
    f’(5) = 2(5) + 4
            = 14
(Jawaban C)

8. Diketahui  dan f’ adalah turunan pertama dari f. Nilai dari f’(1)      = ...

    a.    20
    b.    21
    c.    23
    d.    23
    e.    26
   

Pembahasan


               = 24 – 6 + 6 – 1
               = 23
(Jawaban C)

9. Diketahui . Jika f’ adalah turunan pertama dari f, maka nilai f’(x) = ...

Pembahasan
Kita gunakan rumus ini ya: 


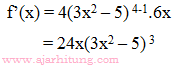(Jawaban D)

10. Total penjualan suatu barang $\left(k\right)$ merupakan perkalian antara harga $\left(p\right)$ dan permintaan $\left(x\right)$ yang dinyatakan dengan $k=px$. Untuk $p=90-3x$ dalam jutaan rupiah dan $1\le x\le 30$, maka total penjualan maksimum adalah...

a. Rp1.350.000.000,00
b. Rp675.000.000,00
c. Rp600.000.000,00
d. Rp450.000.000,00
e. Rp45.000.000,00

Pembahasan

Diberikan $k=px$. Untuk $p=90-3x$, diperoleh
$k=(90-3x)x=-3x^2+90x$
$k$ akan maksimum saat turunan pertamanya, yaitu $\frac{\text{d}k}{\text{d}x}$ bernilai $0$, ditulis
$\begin{array}{cc}\frac{\text{d}k}{\text{d}x}& =-6x+90\\ 0& =-6x+90\\ 6x& =90\\ x& =15\end{array}$
Nilai $x=15$ berada pada interval $x$ yang diberikan.
Substitusikan ke persamaan $k=-3x^2+90x$, sehingga diperoleh
$k_{\text{max}}=-3(15{)}^2+90(15)=675$
Jadi, total penjualan maksimum adalah $675$ juta rupiah atau Rp675.000.000,00
(Jawaban B)

https://mathcyber1997.com/soal-dan-pembahasan-aplikasi-turunan-diferensial/

https://www.ajarhitung.com/2017/02/contoh-soal-dan-pembahasan-tentang_14.html