BARISAN DAN DERET ARITMATIKA BESERTA CONTOH SOAL

Indah Putri Lestari (17)

XI IPS 2

Matematika

BARISAN DAN DERET ARITMATIKA

Baris aritmatika merupakan baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau pengurangan dengan suatu bilangan b. Selisih antara nilai suku-suku yang berdekatan selalu sama yaitu b. Sehingga:

Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmatika dengan nilai:

b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2

Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika dapat diketahui dengan mengetahui nilai suku ke-k dan selisih antar suku yang berdekatan (b). rumusannya berikut ini:

Jika yang diketahui adalah nilai suku pertama  dan selisih antar sukunya (b), maka nilai k = 1 dan nilai  adalah:

Deret aritmatika adalah penjumlahan suku-suku dari suatu barisan aritmatika. Penjumlahan dari suku-suku petama sampai suku ke-n barisan aritmatika dapat dihitung sebagai:

atau sebagai:

Jika hanya diketahui nilai a dalalah suku pertama dan nilai adalah suku ke-n, maka nilai deret aritmatikanya adalah:

Persamaan tersebut bisa dibalik untuk mencari nilai suku ke-n menjadi:

.

.

Sehingga diperoleh .

Contoh soal barisan dan deret aritmatika

Contoh soal 1

Tunjukan bahwa barisan berikut merupakan barisan aritmatika

a. 14, 17, 20, 23, …

b. 40, 35, 30, 25, …

c. x, x + 3, x + 6, x + 9, …

Jawaban : 

Untuk masing-masing barisan di atas tentukan nilai beda terlebih dahulu

a) Dari barisan 14, 17, 20, 23, … diperoleh

U2 – U1 = 17 – 4 = 3

U3 – U2 = 20 – 17 = 3

Karena barisan tersebut mempunyai beda yang tetap, maka barisan tersebut merupakan barisan aritmetika.

b) Dari barisan 40, 35, 30, 25, … diperoleh

U2 – U1 = 35 – 40 = –5

U3 – U2 = 30 – 35 = –5

Karena barisan tersebut mempunyai beda yang tetap, maka barisan tersebut merupakan barisan aritmetika.

c) Dari barisan x, x + 3, x + 6, x + 9, … diperoleh

U2 – U1 = x + 3 – x = 3

U3 – U2 = x + 6 – x + 3 = 3

Karena barisan tersebut mempunyai beda yang tetap, maka barisan tersebut merupakan barisan aritmetika.

Contoh soal 2

Diketahui barisan aritmetika 1, 7, 13, 19, …

a. Tentukan suku ke-10 dan rumus suku ke-n barisan tersebut !

b. Suku keberapakah yang nilainya sama dengan 115 ?

Jawaban :

Contoh soal 3

Pada suatu barisan aritmetika diketahui bahwa suku ke-4 adalah 18 dan suku ke-10 adalah 48.

a. Tentukan suku pertama dan beda dari barisan tersebut !

b. Tentukan rumus suku ke-n barisan tersebut !

Jawaban :

Contoh soal 4

Tentukan suku tengah dari barisan aritmetika 5, 8, 11, 14, … , 77.

Jawaban :

Barisan aritmetika tersebut mempunyai suku pertama a = 5 dan beda b = 3.

Untuk mengetahui suku tengah , terlebih dahulu tentukan banyaknya suku barisan tersebut.

Contoh soal 5

Jika 13, x, 25, y, … merupakan barisan aritmetika, tentukan nilai x dan y adalah. . . .

Jawaban :

Contoh soal 6

diketahui barisan aritmetika 3, 19, 35, … dan antara tiap dua suku yang berurutan disisipkan 3 buah bilangan sehingga terbentuk barisan aritmetika baru

a. Tentukan beda barisan aritmetika baru!

b. Tentukan suku ke-10 dari barisan aritmetika baru!

Jawaban :

Contoh soal 7

Hitunglah nilai dari deret aritmetika 1 + 3 + 5 + … + 153

Jawaban :

Dari deret di atas diperoleh suku pertama a = 1 dan beda b = 3 – 1 = 2, dan suku ke-n adalah Un = 153. Banyaknya suku deret tersebut dicari dengan cara sebagai berikut.

Contoh soal 8

Nilai 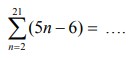 adalah. . .

A. 882

B. 1030

C. 1040

D. 1957

E. 2060

Jawaban : B

Pembahasan : 

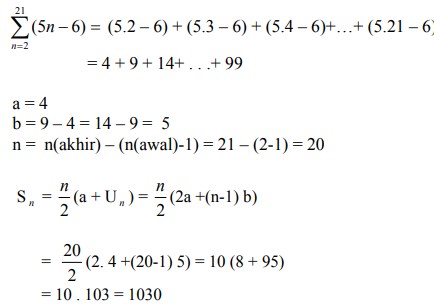
Contoh soal 9

Diketahui 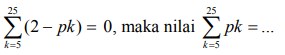  adalah. . .

A. 21

B. 28

C. 30

D. 42

E. 112

Jawaban : A

Pembahasan : 

Contoh soal 10

Suku keempat dan suku ketujuh barisan aritmetika berturut-turut adalah 17 dan 29. Suku ke 25 barisan tersebut adalah….

A. 97

B. 101

C. 105   

D.109   

E. 113

Jawaban : B

Pembahasan : 

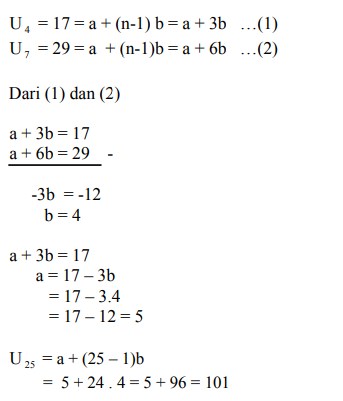
https://www.studiobelajar.com/barisan-deret-aritmatika-geometri/

https://soalkimia.com/soal-barisan-dan-deret-aritmatika/