XI IPS 2
Matematika
PEMBUKTIAN LANGSUNG
Pembuktian langsung adalah metode pembuktian yang menggunakan alur maju. Mulai dari pendefinisian sampai menghasilkan kesimpulan. Gampangnya sih, “kalau A maka B dan kalau B maka C”.
Nah, untuk menggunakan alur maju, maka pernyataan-pernyataan sebelumnya harus benar. Coba deh kamu buktikan pernyataan ini.
“Jumlah dari dua bilangan genap adalah bilangan genap”
Ya... kalau kita pikir-pikir, ya pasti sih, 2 + 2 = 4 dan 4 + 10 = 14. Tapi gimana ya buat bisa membuktikan kalau pernyataan itu berlaku buat semua bilangan genap? Coba perhatikan deh gambar di bawah.

Jadi pertama kamu definisikan dulu tuh bilangan genap itu seperti apa. Bila definisinya sudah benar, lanjut ke pernyataan selanjutnya, maka penjumlahan kedua bilangan itu akan seperti apa. Kamu juga butuh sedikit memanipulasi penjumlahan itu agar bisa mendapat bentuk yang diinginkan.
contoh
1.Buktikan bahwa jumlah dua bilangan ganjil adalah bilangan genap.
Misalkan bilangan tersebut adalah dan . Karena dan ganjil, maka terdapat bilangan bulat dan sedemikian sehingga dan . Dengan menjumlahkan diperoleh
Karena untuk bilangan bulat maka merupakan bilangan genap berdasarkan definisi bilangan genap.
Q.E.D.
Q.E.D.
2. Buktikan bahwa jumlah bilangan genap dan bilangan ganjil adalah bilangan ganjil.
Misalkan bilangan tersebut adalah dan dengan suatu bilangan bulat dan . Jumlahkan dan diperoleh
Karena untuk bilangan bulat , maka adalah bilangan ganjil.
Q.E.D.
Q.E.D.
PEMBUKTIAN TIDAK LANGSUNG
Pembuktian Tidak Langsung Pembuktian tidak langsung atau pembuktian dengan kemustahilan (reductio ad absurdum) yang dibahas ada 2 cara yaitu :
1) kontraposisi
Kontraposisi adalah salah satu metode pembuktian tidak langsung. Kontraposisi memanfaatkan salah satu prinsip dalam logika matematika yaitu

Artinya, kalau mau membuktikan pernyataan p akan menghasilkan pernyataan q itu benar, maka buktikan saja bila bukan q maka akan menghasilkan bukan p. Untuk memahami lebih lanjut coba deh buktikan
“Bila n bilangan bulat dan 7n + 9 bilangan genap, maka n bilangan ganjil”
Misalnya pernyataan p adalah 7n + 9 bilangan genap dan pernyataan q adalah n bilangan ganjil. Maka yang kita buktikan adalah bila n bukan bilangan ganjil (bilangan genap), maka 7n + 9 bukan bilangan genap (bilangan ganjil).

Terbukti kan bila n bukan bilangan ganjil maka 7n + 9 juga bukan bilangan genap? Secara nggak langsung dapat disimpulkan deh bila n bilangan bulat dan 7n + 9 bilangan genap maka n bilangan ganjil.
2) Kontradiksi
Pembuktian tidak langsung dengan kontradiksi dilakukan dengan mengandaikan konklusi yang salah dan menemukan suatu hal yang bertentangan dengan fakta, aksioma, atau teorema yang ada. Pengandaian konklusi salah tidak bisa diterima dan akibatnya konklusi yang ada benar berdasarkan premis yang ada
Contoh Soal :
1. Buktikan untuk setiap n bilangan bulat, jika n ganjil maka n² juga ganjil.
Jawaban : Kita akan membuktikan pernyataan implikasi p → q dengan :
p : n bilangan bulat ganjil,
q : n² bilangan bulat ganjil
Kita awali dengan mengasumsikan ingkarannya benar (p ∩ ∼ q ) yaitu :
p : n bilangan bulat ganjil,
∼ q : n² bilangan bulat genap.
Karena n bilangan bulat ganjil maka bisa kita asumsikan n = 2k + 1 dengan k bilangan bulat. Sehingga :
n² = (2k +1)² = 4k² + 4k + 1 = 2 (2k² + 2k) + 1, Jika kita asumsikan 2k² + 2k = m, Maka persamaan menjadi :
n² = 2m + 1, dari sini bisa dilihat bahwa n² adalah bilangan bulat ganjil. Sehingga kontradiksi dengan asumsi bahwa n² bilangan bulat genap. Asumsi kita salah maka pernyataan semula pastilah benar. Jadi terbukti bahwa untuk setiap n bilangan bulat, jika n ganjil maka n² juga ganjil.
2. Buktikan untuk setiap n bilangan bulat, jika n genap maka n² juga genap
Jawaban : Kita akan membuktikan pernyataan implikasi p → q dengan :
p : n bilangan bulat genap,
q : n² bilangan bulat genap
Kita awali dengan mengasumsikan ingkarannya benar (p ∩ ∼ q ) yaitu :
p : n bilangan bulat genap,
∼ q : n² bilangan bulat ganjil.
Karena n bilangan bulat genap maka bisa kita asumsikan n = 2k dengan k bilangan bulat. Sehingga :
n² = (2k)² = 4k² = 2 (2k²), Jika kita asumsikan 2k² = m, Maka persamaan menjadi :
n² = 2m, dari sini bisa dilihat bahwa n² adalah bilangan bulat genap. Sehingga kontradiksi dengan asumsi bahwa n² bilangan bulat ganjil. Asumsi kita salah maka pernyataan semula pastilah benar. Jadi terbukti bahwa untuk setiap n bilangan bulat, jika n genap maka n² juga genap.
Pembuktian tidak langsung dengan kontradiksi dilakukan dengan mengandaikan konklusi yang salah dan menemukan suatu hal yang bertentangan dengan fakta, aksioma, atau teorema yang ada. Pengandaian konklusi salah tidak bisa diterima dan akibatnya konklusi yang ada benar berdasarkan premis yang ada
Contoh Soal :
1. Buktikan untuk setiap n bilangan bulat, jika n ganjil maka n² juga ganjil.
Jawaban : Kita akan membuktikan pernyataan implikasi p → q dengan :
p : n bilangan bulat ganjil,
q : n² bilangan bulat ganjil
Kita awali dengan mengasumsikan ingkarannya benar (p ∩ ∼ q ) yaitu :
p : n bilangan bulat ganjil,
∼ q : n² bilangan bulat genap.
Karena n bilangan bulat ganjil maka bisa kita asumsikan n = 2k + 1 dengan k bilangan bulat. Sehingga :
n² = (2k +1)² = 4k² + 4k + 1 = 2 (2k² + 2k) + 1, Jika kita asumsikan 2k² + 2k = m, Maka persamaan menjadi :
n² = 2m + 1, dari sini bisa dilihat bahwa n² adalah bilangan bulat ganjil. Sehingga kontradiksi dengan asumsi bahwa n² bilangan bulat genap. Asumsi kita salah maka pernyataan semula pastilah benar. Jadi terbukti bahwa untuk setiap n bilangan bulat, jika n ganjil maka n² juga ganjil.
2. Buktikan untuk setiap n bilangan bulat, jika n genap maka n² juga genap
Jawaban : Kita akan membuktikan pernyataan implikasi p → q dengan :
p : n bilangan bulat genap,
q : n² bilangan bulat genap
Kita awali dengan mengasumsikan ingkarannya benar (p ∩ ∼ q ) yaitu :
p : n bilangan bulat genap,
∼ q : n² bilangan bulat ganjil.
Karena n bilangan bulat genap maka bisa kita asumsikan n = 2k dengan k bilangan bulat. Sehingga :
n² = (2k)² = 4k² = 2 (2k²), Jika kita asumsikan 2k² = m, Maka persamaan menjadi :
n² = 2m, dari sini bisa dilihat bahwa n² adalah bilangan bulat genap. Sehingga kontradiksi dengan asumsi bahwa n² bilangan bulat ganjil. Asumsi kita salah maka pernyataan semula pastilah benar. Jadi terbukti bahwa untuk setiap n bilangan bulat, jika n genap maka n² juga genap.
INDUKSI MATEMATIKA
Induksi matematika menjadi sebuah metode pembuktian secara deduktif yang digunakan untuk membuktikan suatu pernyataan benar atau salah. Dimana merupakan suatu proses atau aktivitas berpikir untuk menarik kesimpulan berdasarkan pada kebenaran pernyataan yang berlaku secara umum sehingga pada pernyataan khusus atau tertentu juga bisa berlaku benar. Dalam induksi matematika ini, variabel dari suatu perumusan dibuktikan sebagai anggota dari himpunan bilangan asli.
Ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan suatu rumus atau pernyataan. Langkah-langkah tersebut adalah :
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1.
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk meyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 kedalam pernyataan P(k).
Jenis Induksi Matematika
Sebagai ilustrasi dibuktikan secara induksi matematika bahwa 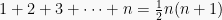 .
.
- Langkah 1
untuk n = 1, maka :
1 = 1
Bentuk untuk n = 1 rumus tersebut benar.
- Langkah 2
Misal rumus benar untuk n = k, maka:
- Langkah 3
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Sehingga:
Pembuktiannya:
tambah k + 1)
- Bilangan bulat hasil pembagian
Suatu bilangan dikatakan habis dibagi jika hasil pembagian tersebut adalah bilangan bulat. Sebagai ilustrasi, dibuktikan secara induksi matematika bahwa 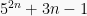 habis dibagi 9.
habis dibagi 9.
Langkah 1
untuk n = 1, maka:
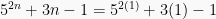

= 27
27 habis dibagi 9, maka n = 1 benar.
Langkah 2
Misal rumus benar untuk n = k, maka :
 (habis dibagi 9)
(habis dibagi 9)
 (b merupakah hasil bagi 5^{2k} + 3k - 1 oleh 9)
(b merupakah hasil bagi 5^{2k} + 3k - 1 oleh 9)
Langkah 3
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Pembuktian:


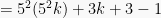
kemudian (5^{2k}) dimodifikasi dengan memasukan



untuk n = 1, maka:
= 27
27 habis dibagi 9, maka n = 1 benar.
Langkah 2
Misal rumus benar untuk n = k, maka :
Langkah 3
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Pembuktian:
kemudian (5^{2k}) dimodifikasi dengan memasukan
contoh
Buktikan bahwa 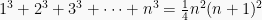 .
.
Pembahasan:
- Langkah 1
- Langkah 2 (n = k)
- Langkah 3 (n = k + 1)

