Indah Putri Lestari (16)
XI IPS 2
Matematika
SOAL PENYELESAIAN PERSAMAAN MATRIKS
Menghitung Determinan Matriks Berordo 3x3
Misalkan, adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.
adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.

Contoh soal 1
Tentukan determinan matriks berikut ini menggunakan aturan Sarrus dan metode minor-kofaktor!

Pembahasan:
- Aturan Sarrus
Agar lebih mudah, kita tulis kembali elemen-elemen pada kolom ke-1 dan ke-2 di sebelah kanan matriks A sebagai berikut:

Kemudian, kita tarik garis putus-putus seperti gambar di atas. Kalikan elemen-elemen yang terkena garis putus-putus tersebut. Hasil kali elemen yang terkena garis putus-putus berwarna biru diberi tanda positif (+), sedangkan hasil kali elemen yang terkena garis putus-putus berwarna oranye diberi tanda negatif (-). Ingat urutan penulisannya juga, ya!

|
Nilai determinan dari matriks A diatas adalah :
A. -6
B. -12
C. 2
D. 10
Pembahasan
|
Maka determinan matriks A adalah ....
A. -9
B. -10
C. -6
D. 8
Pembahasan
Menghitung Determinan Berordo Matriks 2x2
Misalkan, adalah matriks berordo 2x2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.
adalah matriks berordo 2x2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.

|
Nilai determinan dari matriks A di atas adalah ....
A. -2
B. -12
C. 2
D. 10
Pembahasan
|
Jika nilai determinan matriks B adalah 4, maka nilai x adalah ......?
A. 4
B. 3
C. 2
D. 1
Pembahasan
|
|
Agar determinan matriks A sama dengan dua kali determinan B, maka nilai x yang memenuhi adalah....
A. x = -6 atau x = -2
B. x = 6 atau x = -2
C. x = -6 atau x = 2
D. x = 3 atau x = 4
Pembahasan
Keterangan :
KE : Kofaktor Elemen Matriks
a : Baris ke-a
b : Kolom ke-b
NE : Nilai elemen Minor Matriks
Contoh :
Tentukan kofaktor dari minor matriks berikut ini :
KEab = (-1)a+b x NEab
KE11 = (-1)1+1 x NE11 = (-1)2 x (-3) = 1 x -3 = -3
KE12 = (-1)1+2 x NE12 = (-1)3 x (-6) = -1 x (-6) = 6
KE13 = (-1)1+3 x NE12 = (-1)4 x (-3) = 1 x (-3) = -3
KE21 = (-1)2+1 x NE21 = (-1)3 x (-6) = -1 x (-6) = 6
KE22 = (-1)2+2 x NE22 = (-1)4 x (-12) = 1 x (-12) = -12
KE23 = (-1)2+3 x NE23 = (-1)5 x (-6) = -1 x (-6) = 6
KE31 = (-1)3+1 x NE31 = (-1)4 x (-3) = 1 x (-3) = -3
KE32 = (-1)3+2 x NE32 = (-1)5 x (-6) = -1 x (-6) = 6
KE33 = (-1)3+3 x NE33 = (-1)6 x (-3) = 1 x (-3) = -3
Maka kofaktornya adalah :
Mencari invers matriks berordo 3x3 dapat dilakukan dengan dua cara, yaitu dengan adjoin dan transformasi baris elementer. Hm, kira-kira seperti apa ya penjelasan lebih detailnya. Mari kita bahas satu persatu, ya.
- Invers matriks ordo 3x3 dengan adjoin
Pada penjelasan sebelumnya tentang determinan matriks, kamu udah tau kan bagaimana cara mencari kofaktor dari suatu matriks. Nah, dari kofaktor-kofaktor tersebut, kita dapat menentukan adjoin matriksnya, lho. Adjoin matriks merupakan transpose dari suatu matriks yang elemen-elemennya merupakan kofaktor dari elemen-elemen matriks tersebut.

Contoh soal 1
Tentukan invers matriks berikut dengan menggunakan adjoin!

Penyelesaian:

Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:

Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.

Oleh karena itu,

Jadi,



Contoh soal 1
Tentukanlah invers dari matriks berikut.

Pembahasan:

Catatan: elemen-elemen yang berada di lingkar biru merupakan diagonal utama matriks A yang ditukar posisinya, sedangkan elemen-elemen yang berada di lingkar oranye merupakan diagonal kedua matriks A yang dikalikan dengan minus satu (-1).
Contoh soal 2
Menentukan matriks invers dari:
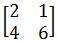
Jawaban:

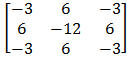
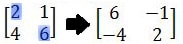
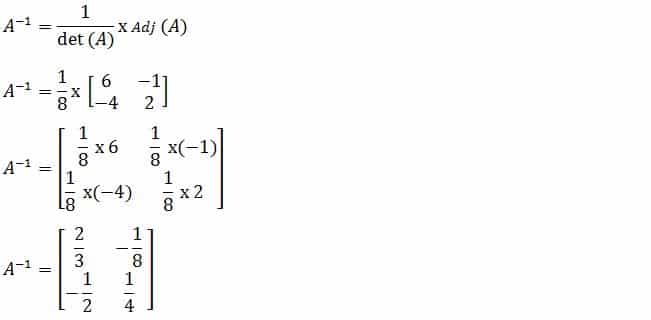


Tidak ada komentar:
Posting Komentar